Union

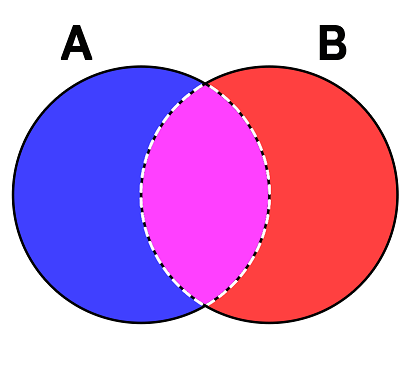
The Union node takes the union of items found in two Sets, assigning the union to a Resultant Set, with the result containing items found in both Set A and Set B. Visually, the intersection of Set A and Set B looks like the following diagram, where the intersection of Set A and Set B contains items that are common to both Sets.

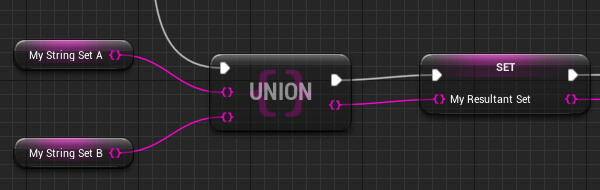
For illustrative purposes, let's say that you have two string type Sets, Set A and Set B, both of which are defined below.

	Set A = {"Item 1", "Item 2", "Item 3", "Item 4", "Item 5"}
	Set B = {"Item 4", "Item 5", "Item 6", "Item 7", "Item 8"}
Copy full snippet

Set A = {"Item 1", "Item 2", "Item 3", "Item 4", "Item 5"} Set B = {"Item 4", "Item 5", "Item 6", "Item 7", "Item 8"}

The following table shows you the result, which contains the union of Set A and Set B (symbolically represented as A ∪ B).

A Set is a collection of unique items, which means that duplicate items will be eliminated from the Resultant Set.

Inputs

Outputs

Example Usage

Footnote

Symbolically, this operation is represented as A ∪ B = { x | x ∈ A ∨ x ∈ B }, wherein this node is performing a logical OR operation between elements in Set A and elements in Set B.