머티리얼 데이터 타입 페이지에서는 머티리얼 에디터에서 데이터를 나타내는 4가지 방법을 소개했습니다. 효과적으로 머티리얼을 생성하려면 이러한 데이터 타입은 물론 데이터를 조작하고 머티리얼 그래프를 통해 정보가 이동하는 방식을 제어하는 방법을 알아야 합니다.
이 문서에서는 두 가지 주제에 관해 설명합니다.
- 데이터 타입 조작: 플로트를 멀티 채널 벡터로 결합하는 방법과 반대로 더 큰 데이터 타입에서 정보를 분리하는 방법.
- 머티리얼 그래프 산술: 머티리얼 그래프에서 여러 데이터 타입과의 산술 연산을 수행하기 위한 규칙 및 프로세스.
데이터 타입 조작
한 데이터 타입에서 일부 정보가 유래한다는 이유로 해당 데이터 타입을 유지해야 하는 것은 아닙니다. 예를 들어 2개의 스칼라 파라미터(floats)를 2채널 벡터(float2)로 결합 또는 덧붙이기 하여 2채널 데이터가 필요한 입력에 전달할 수 있습니다. 반대로 ComponentMask 를 사용하여 더 큰 벡터에서 채널의 특정 서브셋을 얻을 수 있습니다.
이 섹션에서 설명하는 머티리얼 표현식은 정보가 머티리얼 그래프를 이동하는 방식을 제어하기 위해 데이터를 결합 및 분리하는 방법을 제공합니다.
AppendVector
AppendVector 머티리얼 표현식은 입력 A 의 데이터와 입력 B 의 데이터를 결합하고, 멀티 채널 벡터(float2, float3 또는 float4)를 출력합니다. 이 예시에서는 2개의 상수가 덧붙여져 float2를 출력합니다. (1, 2)

예시 사용 사례
Append 노드는 2개의 값을 개별적으로 수정한 다음 멀티 채널 데이터가 필요한 입력에 이 값들을 전달해야 할 때 유용합니다. 아래 그래프에는 아티스트가 머티리얼 인스턴스에 있는 텍스처의 타일링 또는 UV 스케일 을 제어하는 방법이 나와 있습니다. 단, 균등한 제어만 가능합니다.

이 예시에서의 단점은 머티리얼 그래프에 1개의 파라미터만 포함되어 있으면서 UV 좌표에는 2개의 채널이 있다는 것입니다. 이 솔루션을 사용하면 텍스처의 너비와 높이를 개별적으로 제어할 수 없습니다.
AppendVector 를 사용하여 이를 해결할 수 있습니다. 각 축에 대해 별도의 스칼라 파라미터를 생성한 다음 이를 Append 노드에 전달합니다. Append 노드는 2개의 파라미터를 float2에 결합한 다음 float2에 텍스처 좌표를 곱합니다.

타일링 X 와 타일링 Y 가 별도로 파라미터화되므로 텍스처의 너비와 높이를 이제 개별적으로 제어할 수 있습니다.
덧붙이기 순서
AppendVector 표현식은 노드에 연결된 순서대로 데이터를 결합합니다. 입력 B의 데이터가 항상 입력 A에 있는 데이터의 끝에 덧붙여집니다. 아래의 두 이미지를 참조하세요.

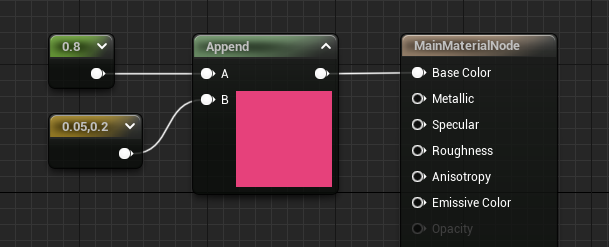
- 첫 번째 슬라이드에서 덧붙여진 결과는 (0.05, 0.2, 0.8) 또는 노드 프리뷰에 표시된 것처럼 연한 파랑입니다.
- 두 번째 슬라이드에서 덧붙여진 결과는 (0.8, 0.05, 0.2) 또는 노드 프리뷰에 표시된 것처럼 분홍색입니다.
AppendMany
AppendMany 는 AppendVector 표현식과 동일한 방식으로 작동하는 머티리얼 함수지만, 최대 4개의 별도 플로트/스칼라 값을 멀티 채널 벡터로 결합할 수 있습니다.

AppendMany 함수의 추가적인 이점으로는 3개의 서로 다른 출력 핀을 제공한다는 것이 있습니다. 이를 통해 주어진 상황에 따라 덧붙여진 채널 중 일부 또는 모두에 액세스할 수 있습니다.
AppendMany 노드는 입력에 플로트/스칼라 값만 수락합니다. float2, float3 또는 float4를 AppendMany 노드에 전달하는 경우 첫 번째 이외의 값은 폐기됩니다.
Component Mask
Component Mask 머티리얼 표현식은 위에서 설명한 Append 노드와 목적이 반대입니다. ComponentMask는 데이터를 결합하는 대신 데이터를 컴포넌트 파트 또는 채널로 분리할 수 있습니다.
Component Mask 함수는 게이트와 같은 역할을 합니다. 입력에 연결된 모든 데이터에 대해 출력을 통해 전달이 허용되는 채널을 정확하게 선택할 수 있습니다. 아래 이미지는 (0, 1, 0.7, 0.5) 값이 포함된 Constant4Vector를 나타냅니다. 그래프에서 Mask 노드를 선택할 때 디테일(Details) 패널에 4개의 체크 박스가 표시됩니다.

이 체크 박스는 노드가 출력되는 채널을 결정합니다. 현재는 아무 것도 선택되어 있지 않으므로 Mask 노드는 어떠한 정보도 출력하지 않습니다. 다운스트림 입력에 연결을 시도하는 경우 노드에 오류가 표시됩니다.

이 체크 박스를 통해 정보를 필터링하고 필요한 채널만 사용할 수 있습니다.
A 채널 의 값을 사용하여 머티리얼의 오파시티를 제어하고자 한다고 가정하겠습니다. 체크 박스를 선택하여 A 채널을 활성화한 다음 Mask의 출력 핀을 Opacity Input 에 연결합니다.

ComponentMask는 선택되지 않은 R, G, B 채널을 폐기하고, A 채널의 값(이 경우 0.5)만 출력합니다.
머티리얼 그래프 산술
머티리얼 그래프에서 데이터를 조작하는 두 번째 주된 방식은 산술 연산을 이용하는 것입니다. 모든 일반적인 산술 연산은 머티리얼 에디터에서 가능합니다.

4개의 산술 머티리얼 표현식이 있습니다. 수학 머티리얼 표현식 페이지에서 자세히 알아보세요.
산술 노드의 기본 목적은 비교적 명확해야 합니다. 예를 들어 0.3 과 0.2 의 상수 값을 Add 노드에 연결해야 하는 경우 Add 노드는 0.3 + 0.2 를 계산하고 0.5 의 값을 출력합니다. 두 상수 값 간 산술은 간단하고 직관적입니다.

하지만 데이터 타입 페이지에 나와 있는 것과 같이 정보가 항상 개별 플로트 값처럼 머티리얼 그래프를 이동하는 것은 아닙니다. 이로 인해 머티리얼에 있는 다양한 데이터 타입 간 산술을 수행하는 데 있어 규칙과 프로세스를 이해하는 것이 중요합니다. 다음 두 가지 사항에 유의해야 합니다.
- 산술 연산에서 모든 데이터 타입이 서로 호환되는 것은 아닙니다.
- 산술 연산은 데이터 타입에 따라 다르게 작동합니다.
호환 및 비호환 데이터 타입
위의 예시에서는 두 플로트 값 간 단순 덧셈 연산(0.3 + 0.2 = 0.5)을 보여주었습니다. 이 연산은 두 값이 모두 같은 종류의 데이터이기 때문에 작동합니다. 입력 중 하나에 다른 데이터 타입이 전달되면 어떻게 될까요? 데이터 타입 간 호환성은 다음과 같은 세 가지로 요약할 수 있습니다.
-
같은 데이터 타입 간 산술은 항상 유효합니다. 예를 들어 float2 + float2 는 새로운 float2를 반환합니다.
-
플로트와 더 큰 플로트 간 산술은 유효합니다. 예를 들어 float + float3 는 새로운 float3 를 반환합니다.
-
2개의 서로 다른 데이터 타입 간 산술은 유효하지 않습니다. 예를 들어 float2 + float3 는 유효하지 않고 오류를 반환합니다.
다시 말해 2개의 서로 다른 데이터 타입 간 산술은 가능하지만 데이터 타입 중 하나가 float인 경우에 한합니다. 아래 그래프에서 연산 0.3 + (1,2) 는 유효합니다. float가 float2의 두 값 모두에 더해지고, 결과는 값이 (1.3, 2.3) 인 새로운 float2가 됩니다.

하지만 서로 다른 float2, float3 또는 float4 데이터 간 산술은 오류를 반환합니다.

아래 표에 머티리얼 그래프 산술의 데이터 타입 호환성이 요약되어 있습니다.
| 데이터 타입 | 산술에 호환되는 데이터 타입 |
|---|---|
| Float | 모두 |
| Float2 | Float, Float2 |
| Float3 | Float, Float3 |
| Float4 | Float, Float4 |
데이터 타입 간 산술 규칙
다른 데이터 타입 간 산술 계산이 어떻게 수행되는지도 이해해야 합니다. 아래 두 시나리오에서는 데이터 타입 중 하나 또는 둘 모두가 플로트보다 클 때 산술이 어떻게 이루어지는지 보여줍니다.
같은 데이터 타입 간 산술
같은 데이터 타입(예: float2 + float2) 간 산술에서 입력 A의 각 값은 입력 B의 해당하는 값으로 연산됩니다. 아래 예시에서는 두 Constant2Vector 표현식 간 덧셈을 보여줍니다.

긴 양식으로 작성하면 2개의 개별 덧셈 연산이 있습니다. 각 노드의 첫 번째 값이 더해집니다. (1 + 2). 그런 다음 각 노드의 두 번째 값이 더해집니다. (3 + 3). 결과는 새로운 float2가 됩니다. (2, 6)
아래 차트에는 4가지 데이터 타입 각각에 대한 산술 예시가 나와 있습니다.
| 입력 A, 입력 B | 입력 데이터 | 수학적 표기 | 결과 데이터 |
|---|---|---|---|
| Float, Float | (4) / (2) | 4 / 2 = 2 | 8 |
| Float2, Float2 | (1, 3) + (2, 3) | (1 + 2), (3 + 3) | (3, 6) |
| Float3, Float3 | (3, 2, 0.5) * (2, 1, 2) | (3 x 2), (2 x 1), (0.5 x 2) | (6, 2, 1) |
| Float4, Float4 | (2, 2, 2, 3) - (1, 1, 2, 2,) | (2 - 1), (2 - 1), (2 - 2), (3 - 2) | (1, 1, 0, 1) |
플로트와 벡터 간 산술
플로트와 더 큰 데이터 타입 간에 산술이 이루어질 때 각 별도의 계산에 플로트가 반복적으로 사용됩니다. 아래 이미지에서는 Constant 와 Constant3Vector 가 곱해집니다.

그림에 나와 있는 것과 같이 Constant의 값이 Constant3Vector에 있는 각각의 값과 곱해집니다. 3개의 개별적인 곱셈 표현식이 있습니다. (2 3), (2 1), (2 *2). 결과는 float3입니다. (6, 2, 4)
입력 A 또는 입력 B의 플로트는 곱셈 및 덧셈과 연관이 없더라도 나눗셈 및 뺄셈과는 연관이 있습니다.

위 이미지에서는 Constant (2)의 값을 Constant3Vector (6, 4, 3)의 각 값에서 뺍니다. 수학적 표기로 작성하면 다음과 같습니다. (6 - 2), (4 - 2), (3 - 2). 결과는 float3 (4, 2, 1) 입니다.
입력 순서를 반전하는 경우 결과가 달라집니다.

float가 Subtraction 노드의 윗부분이므로 각 산술 연산은 반전됩니다. (2 - 6), (2 - 4), (2 - 3) 결과는 float3 (-4, -2, -1) 입니다.
결론
이 페이지의 개념과 기술은 머티리얼 생성에 사용되는 대부분의 머티리얼 그래프 로직에서 주요한 구성 요소입니다. 아래에 링크된 레퍼런스 페이지는 머티리얼 에디터에서의 수학 및 데이터 조작 연산을 이해하는 데 도움이 될 수 있습니다.
