Union

Union ノードは 2 つの Set に含まれるアイテムをすべて集め、その和集合を Resultant Set に割り当てて、結果が Set A と Set B の両方に属するアイテムとなるようにします。 Set A と Set B の共通部分を図で表すと以下のようになります。この場合、Set A と Set B の共通部分は両方の Set に共通するアイテムです。

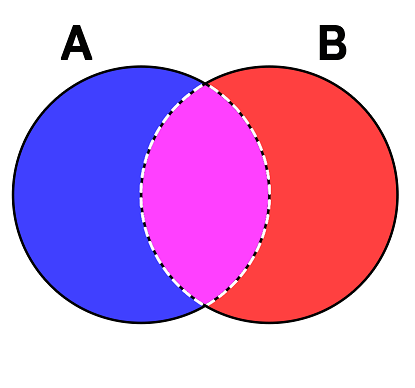
解説しやすいように、Set A と Set B という 2 つのストリング型をそれぞれ以下のように定義します。

	Set A = {"Item 1", "Item 2", "Item 3", "Item 4", "Item 5"}
	Set B = {"Item 4", "Item 5", "Item 6", "Item 7", "Item 8"}
Copy full snippet

Set A = {"Item 1", "Item 2", "Item 3", "Item 4", "Item 5"} Set B = {"Item 4", "Item 5", "Item 6", "Item 7", "Item 8"}

は以下の表は、Set A and Set B の和集合が含まれる結果を表します (記号で表すと A ∪ B)。

Set はユニークなアイテムのコレクションです。つまり、重複アイテムは Resultant Set から取り除かれます。

入力

出力

使用例

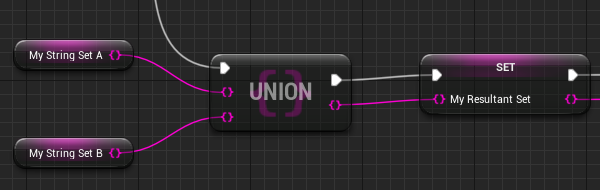
補足説明

この演算を記号で表すと A ∪ B = { x | x ∈ A ∨ x ∈ B } となり、このノードは、Set A のエレメントと Set B のエレメントの間で論理 OR 演算を実行します。